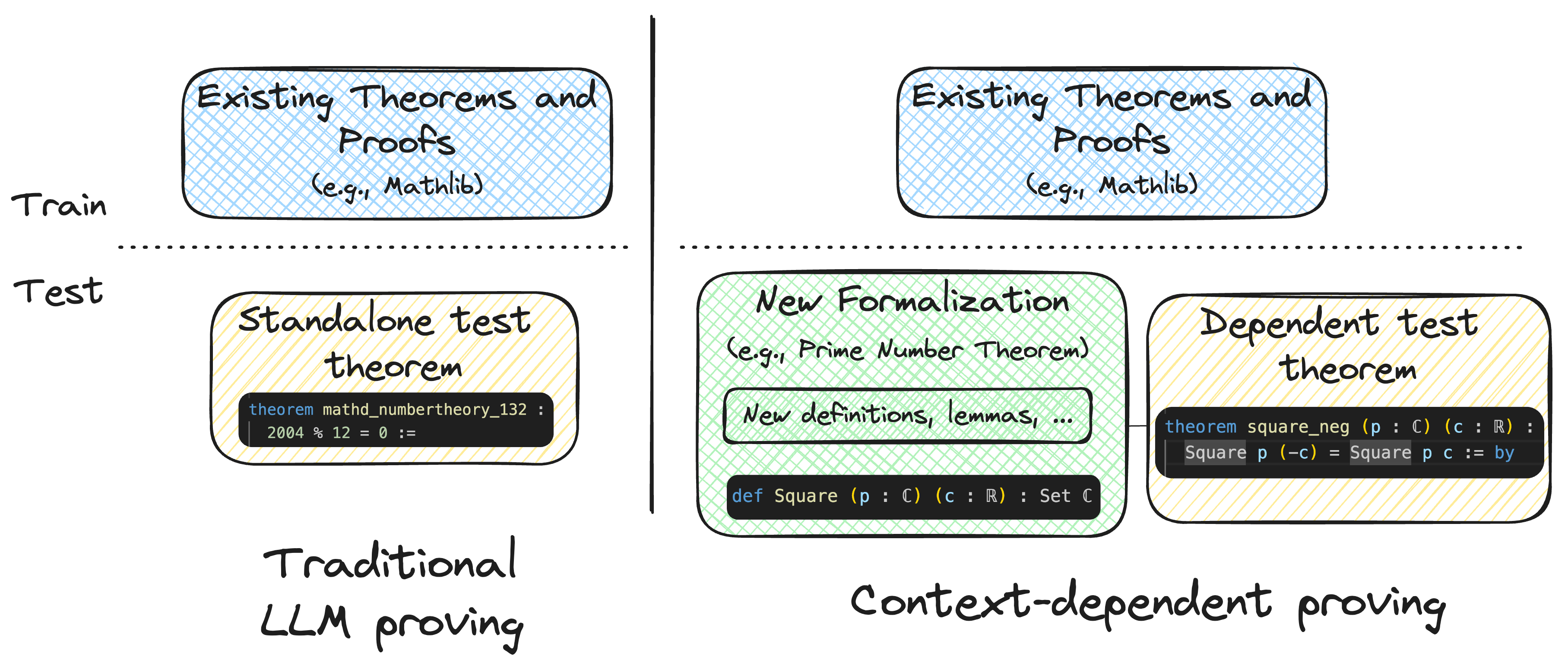
Real-world formal theorem proving often depends on a wealth of context, including definitions, lemmas, comments, file structure, and other information. We introduce miniCTX, which tests a model's ability to prove formal mathematical theorems that depend on new context that is not seen during training.
miniCTX contains theorems sourced from real Lean projects and textbooks, each associated with a context that can span tens of thousands of tokens. Models are tasked with proving a theorem given access to code from the theorem's repository, which contains context that is needed for the proof. As a baseline for miniCTX, we tested fine-tuning and prompting methods that condition theorem proving on preceding context. Both approaches substantially outperform traditional methods that rely solely on state information.
We found that this ability to use context is not captured by previous benchmarks such as miniF2F. Alongside miniCTX, we offer ntp-toolkit for automatically extracting and annotating theorem proving data, making it easy to add new projects into miniCTX to ensure that contexts are not seen during training. miniCTX offers a challenging and realistic evaluation of neural theorem provers.
Unlike popular benchmarks that focus on isolated competition problems, miniCTX includes complex theorems from a variety of ongoing Lean projects, like the Prime Number Theorem and the Polynomial Freiman-Ruzsa Conjecture. This diversity tests a model's ability to generalize in real-world formalization projects.
miniCTX includes theorems along with new context, such as definitions, lemmas, and comments, which may make some theorems easier to prove. This contextual information helps evaluate whether models can leverage real-world context beyond standalone proofs.
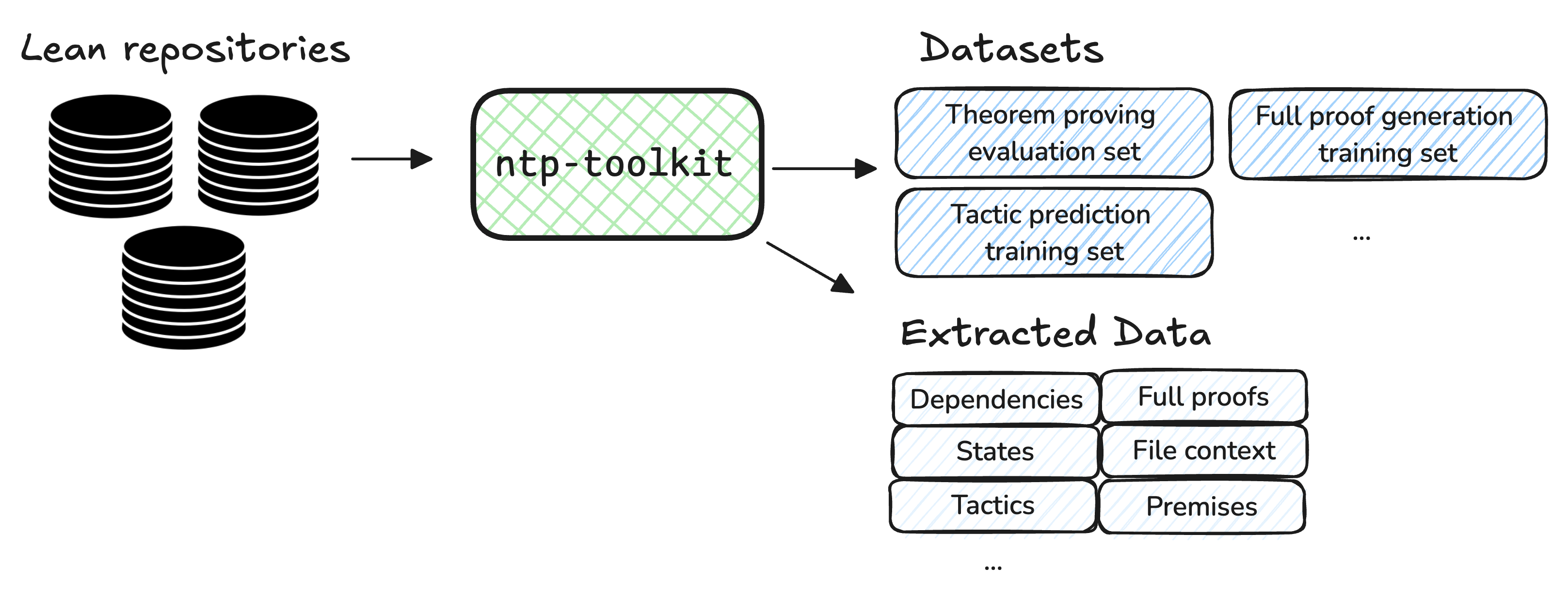
miniCTX ensures that evaluation data is kept fresh by automatically updating the benchmark with new Lean projects using ntp-toolkit. This prevents data contamination from evaluating models and maintains a realistic evaluation setting.
Each theorem in miniCTX consists of three main components: the theorem statement, preceding file contents, and metadata in JSON format. These elements provide the complete context required for proving the theorem.
Users can reconstruct the complete context for each theorem using the metadata, which includes both in-file and cross-file context, enabling realistic and comprehensive evaluation.
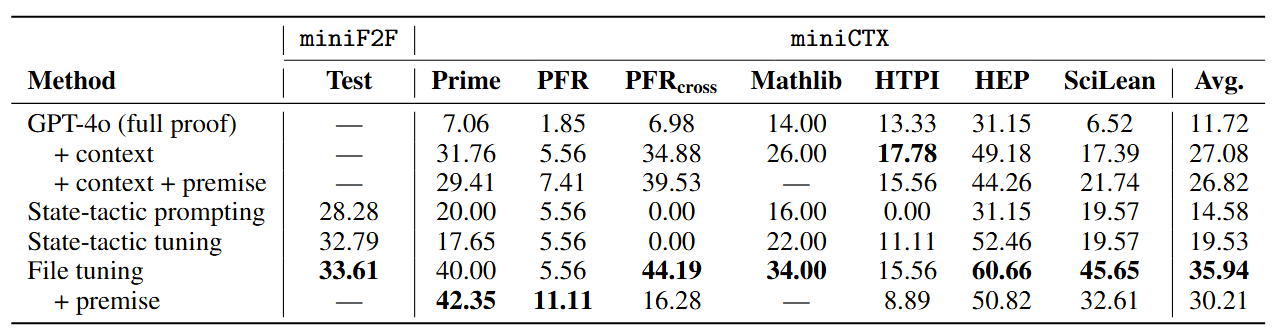
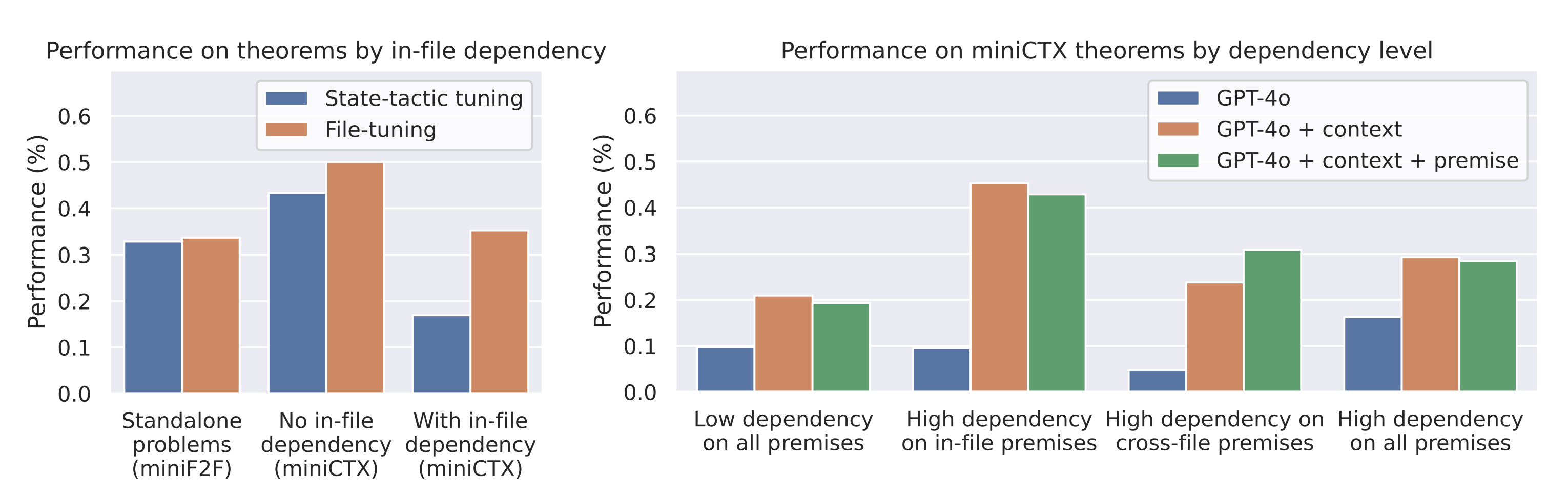
Our experiments evaluate the effectiveness of various baseline models on the miniCTX benchmark. We find that models utilizing richer context information significantly outperform those relying solely on proof states. Specifically, the file-tuned model, which incorporates full file context, achieves an average success rate of 35.94%, compared to 19.53% for state-tactic models trained without context. Adding relevant premises also improves performance in scenarios requiring high cross-file dependency, as seen with GPT-4o on datasets like PFR and SciLean. These results highlight the value of providing comprehensive context, demonstrating that miniCTX effectively captures the importance of both in-file and cross-file context in formal theorem proving.
The NTP Toolkit is an automated tool for extracting training and evaluation data from Lean repositories with minimal manual effort. It transforms Lean 4 repositories into next-tactic or full proof examples, enabling seamless fine-tuning and evaluation of language models. All problems and training data for miniCTX are automatically extracted using the toolkit. The toolkit also generates instruction-tuning data with natural language instructions to facilitate task learning. To learn more, visit the GitHub repository.
@article{hu2024minictx,
title={miniCTX: Neural Theorem Proving with (Long-) Contexts},
author={Hu, Jiewen and Zhu, Thomas and Welleck, Sean},
journal={arXiv preprint arXiv:2408.03350},
year={2024}
}