Consistency of language models with respect to incomplete decoding algorithms
Related publications
2023
-
Nouha Dziri, Ximing Lu, Melanie Sclar, and 13 more authors
In Thirty-seventh Conference on Neural Information Processing Systems, Jul 2023
2022
-
Daniel Khashabi, Xinxi Lyu, Sewon Min, and 8 more authors
In Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Jul 2022
Fine-tuning continuous prompts for target tasks has recently emerged as a compact alternative to full model fine-tuning. Motivated by these promising results, we investigate the feasibility of extracting a discrete (textual) interpretation of continuous prompts that is faithful to the problem they solve. In practice, we observe a “wayward” behavior between the task solved by continuous prompts and their nearest neighbor discrete projections: We can find continuous prompts that solve a task while being projected to an arbitrary text (e.g., definition of a different or even a contradictory task), while being within a very small (2%) margin of the best continuous prompt of the same size for the task. We provide intuitions behind this odd and surprising behavior, as well as extensive empirical analyses quantifying the effect of various parameters. For instance, for larger model sizes we observe higher waywardness, i.e, we can find prompts that more closely map to any arbitrary text with a smaller drop in accuracy. These findings have important implications relating to the difficulty of faithfully interpreting continuous prompts and their generalization across models and tasks, providing guidance for future progress in prompting language models.
2021
-
Lang Liu, Krishna Pillutla, Sean Welleck, and 3 more authors
In Advances in Neural Information Processing Systems, Jul 2021
-
Ilia Kulikov, Sean Welleck, and Kyunghyun Cho
In Proceedings of the 5th Workshop on Structured Prediction for NLP (SPNLP 2021), Aug 2021
Despite its wide use, recent studies have revealed unexpected and undesirable properties of neural autoregressive sequence models trained with maximum likelihood, such as an unreasonably high affinity to short sequences after training and to infinitely long sequences at decoding time. We propose to study these phenomena by investigating how the modes, or local maxima, of a distribution are maintained throughout the full \textitlearning chain of the ground-truth, empirical, learned and decoding-induced distributions, via the newly proposed \textitmode recovery cost. We design a tractable testbed where we build three types of ground-truth distributions: (1) an LSTM based structured distribution, (2) an unstructured distribution where probability of a sequence does not depend on its content, and (3) a product of these two which we call a semi-structured distribution. Our study reveals both expected and unexpected findings. First, starting with data collection, mode recovery cost strongly relies on the ground-truth distribution and is most costly with the semi-structured distribution. Second, after learning, mode recovery cost from the ground-truth distribution may increase or decrease compared to data collection, with the largest cost degradation occurring with the semi-structured ground-truth distribution. Finally, the ability of the decoding-induced distribution to recover modes from the learned distribution is highly impacted by the choices made earlier in the learning chain. We conclude that future research must consider the entire learning chain in order to fully understand the potentials and perils and to further improve neural autoregressive sequence models.
2020
-
Sean Welleck, Ilia Kulikov, Jaedeok Kim, and 2 more authors
In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Nov 2020
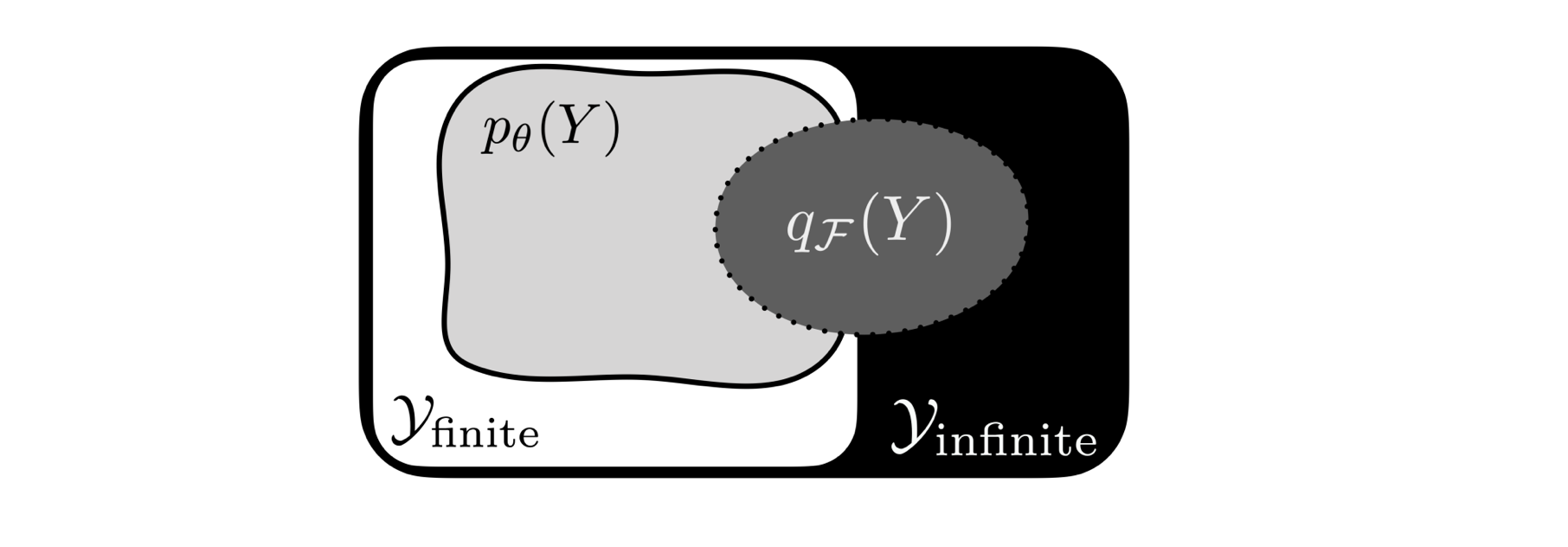
Despite strong performance on a variety of tasks, neural sequence models trained with maximum likelihood have been shown to exhibit issues such as length bias and degenerate repetition. We study the related issue of receiving infinite-length sequences from a recurrent language model when using common decoding algorithms. To analyze this issue, we first define inconsistency of a decoding algorithm, meaning that the algorithm can yield an infinite-length sequence that has zero probability under the model. We prove that commonly used incomplete decoding algorithms – greedy search, beam search, top-k sampling, and nucleus sampling – are inconsistent, despite the fact that recurrent language models are trained to produce sequences of finite length. Based on these insights, we propose two remedies which address inconsistency: consistent variants of top-k and nucleus sampling, and a self-terminating recurrent language model. Empirical results show that inconsistency occurs in practice, and that the proposed methods prevent inconsistency.